「a と b が点のとき, ab は a と b を通る直線,
a と b が直線のとき, ab は a と b の交点,
a が点で b が直線のとき, ab は a から b への垂線。」
点または直線
「三つとも点のときは一直線上にあり, 三つとも直線のときは一点で交わるか互いに平行であり,
二つが点で残りの一つが直線のときは 2点を通る直線が残りの直線に直交し,
二つが直線で残りの一つが点のときは 2直線が平行である。」
「AA', BB', CC' が従属していれば, (BC)(B'C'), (CA)(C'A'), (AB)(A'B') も従属している。」 が成り立ちます。
A, B, C, A', B', C' がすべて点のときが デザルグの定理です。
A, B, C が点で a', b', c' が直線のときに、 b'c', c'a', a'b' をそれぞれ A', B', C' に置き換えたものが, 定理 1 です。 この定理はある本に書いてありました。
A, B', C' が点で b, c, a' が直線のときに B', C', bc, ca', a'b をそれぞれ B, C, A', B', C' に置き換えると
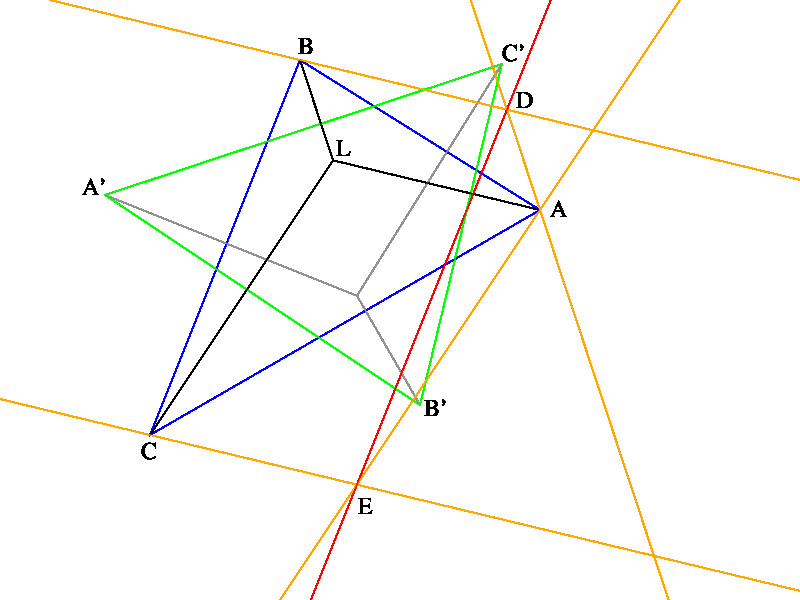
「A, B, C からそれぞれ B'C', C'A', A'B' への垂線が一点 L で交われば,
A から A'C' への垂線と B から B'C' への垂線の交点を D,
A から A'B' への垂線と C から B'C' への垂線の交点を E とすれば,
DE は BC に平行である。(左下図)」となります。
ここで, BD と CE が平行であることに注意すれば DE = BC となります。
また, B'C' への垂線は AL に平行な直線であることに注意すれば, 以下の定理が得られます。
三角形 ABC と点 L があるとき, 点 D, E, F を BLCD, CLAE, ALBF がそれぞれ平行四辺形となるようにとれば, ⊿DEF ≡ ⊿ABC である。」
証明は簡単です。
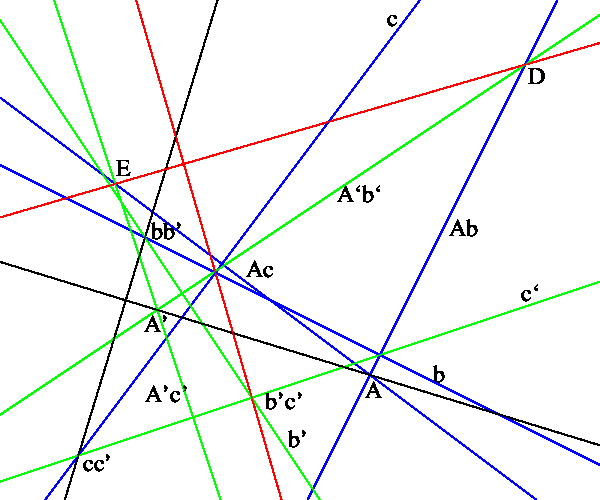
A, A' が点で, b, c, b', c' が直線のときは
「bb' と cc' を通る直線が AA' に直交していれば,
A から b への垂線と A' から b' への垂線の交点を D,
A から c への垂線と A' から c' への垂線の交点を E とすれば,
bc と b'c' を通る直線が DE に直交している。(右上図)」
となります。
a, b, c, l のそれぞれが点または直線のとき, 「((al)l)(bc), ((bl)l)(ca), ((cl)l)(ab) が従属している。」から, 以下の五つの定理が得られます。
(
(AL)L は L を通って AL に直交する直線であり,
(al)l は al を通って l に直交する直線であり,
(Al)l は A から l へ下ろした垂線の足であり,
(aL)L は L を通って a に平行な直線です。
定理 2 定理 3 定理 4 定理 5 定理 6
最初の 定理 2 はある本に書いてありましたが, 他の四つは見たことがありません。
a, b, c, l がすべて直線のときは
「al を通って l に直交する直線へ bc から下ろした垂線,
bl を通って l に直交する直線へ ca から下ろした垂線,
cl を通って l に直交する直線へ ab から下ろした垂線は一点で交わるか互いに平行である。」
となりますが, 上の三垂線は(ユークリッド幾何学では) l に平行ですから, あたりまえの命題になってしまいます。
a, b, c が直線で L が点のときは
「L を通って a に平行な直線へ bc から下ろした垂線,
L を通って b に平行な直線へ ca から下ろした垂線,
L を通って c に平行な直線へ ab から下ろした垂線は一点で交わる。」
となりますが, 上の三垂線は(ユークリッド幾何学では) bc, ca, ab からそれぞれ a, b, c への垂線に他なりませんから、三辺形 abc の垂心で交わります。
「a, c, e が従属し, b, d, f も従属すれば, (ab)(de), (bc)(ef), (cd)(fa) も従属する。」 が 成り立ちます。
A, B, C, D, E, F がすべて点のときがパップスの定理で, a, b, c, d, e, f がすべて直線のときがパップスの定理の双対命題です。
A, B, C, D, E が点で f だけが直線のとき, Ef は E から f への垂線ですが, BD が f に直交するので E を通って BD に平行な直線であることに注意すれば, 次の定理になります。
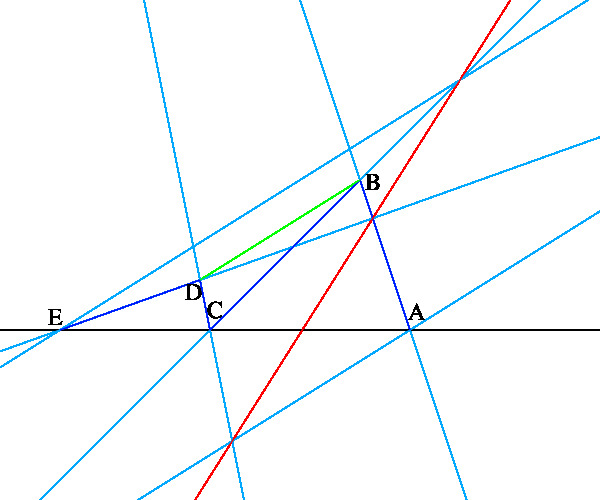
「5点 A, B, C, D, E のうち A, C, E が一直線上にあれば,
AB と DE の交点,
E を通って BD に平行な直線と BC の交点,
A を通って BD に平行な直線と CD の交点は一直線上にある(下図参照)。」
(
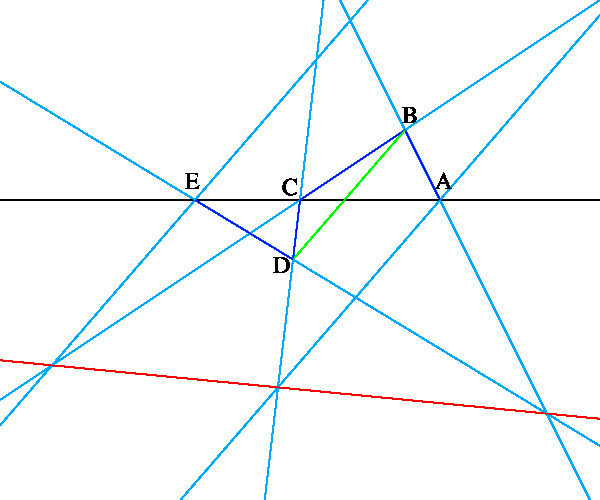
A, B, D, E が点で c, f が直線のとき, A を P, (cD)(fA) を Q, D を R, B を S, (Bc)(Ef) を T, E を U に置き換えれば, 次の定理になります。
「六角形 PQRSTU において PQ, RS, TU が互いに平行であり, QR, ST, UA も互いに平行ならば, PS, QT, RU は一点で交わる。」
(